Der Profilbereich Space, Time & Matter erforscht in sechs Forschungsschwerpunkten die physikalischen und mathematischen Grundlagen der Naturwissenschaften: von den elementaren Bausteinen der Materie, die die Teilchen-, Kern- und Atomphysik untersucht, bis hin zum Zusammenwirken der Bausteine in Festkörpern, künstlich herstellbaren Quantenmaterialien, in der Atmosphäre und dem Inneren von Erde, Planeten und Neutronensternen. Dazu erforderlich sind mathematisch präzise und effiziente Methoden und Algorithmen.

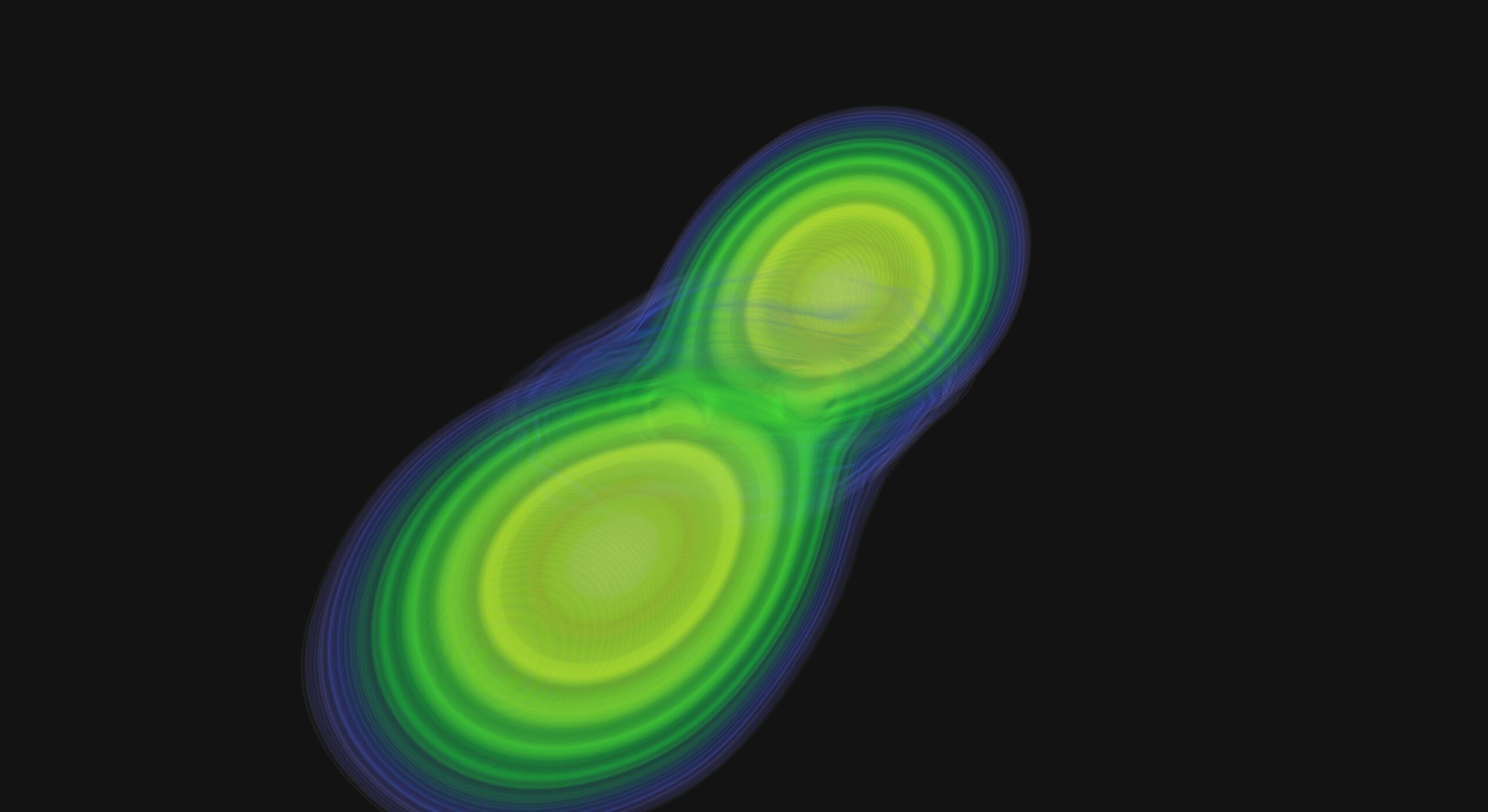
Extreme Zustände
Wer verstehen will, warum es im Universum schwere Elemente gibt, muss Neutronensterne, Kilonovae und Gravitationswellen erkunden. Im Clusterprojekt ELEMENTS haben sich rund hundert Teilchen- und Astrophysiker*innen mit diesem Ziel zusammengeschlossen.
Unser Universum ist voller Extreme: In unvorstellbar weiter Entfernung kollidieren unglaublich massive und kompakte Objekte, um die allerwinzigsten Teilchen freizusetzen. Genau diese extremen Phänomene sind ein zentrales Thema des Forschungsprojekts ELEMENTS (Exploring the Universe from Microscopic to Macroscopic Scales). Theoretiker*innen und Experimentator*innen arbeiten gemeinsam an der Frage, wie schwere Elemente, zum Beispiel Kupfer, Gold und Blei, im Universum entstehen. »Wir betreiben Grundlagenforschung – denn Gold ist überall um uns herum, aber es ist nicht auf unserem Planeten entstanden«, erklärt ELEMENTS-Sprecher Professor Luciano Rezzolla vom Institut für Theoretische Physik an der Goethe-Universität. »Es kommt aber auch nicht aus den Sternen, die nur sehr wenig schwere Elemente produzieren.« Das rund 100-köpfige Team von Goethe-Universität, TU Darmstadt, Universität Gießen und GSI Helmholtzzentrum für Schwerionenforschung (GSI) möchte also im Prinzip wissen, woher unser Gold kommt.
Dafür braucht es einige Zutaten und viel Zeit. Am Ende seines langen Lebens kollabiert ein Stern unter seiner eigenen Schwerkraft und explodiert als Supernova. Dabei werden Gas, Staub und jede Menge Energie in den umliegenden Raum geschleudert. Später sind diese Überreste als Nebel mit faszinierenden Formen und Farben sichtbar. Je nachdem, wie massereich (»groß«) der Stern ursprünglich war, entsteht ein stellares Schwarzes Loch oder ein Neutronenstern. Während die Schwarzen Löcher weithin bekannt sind, werden ihre kleinen Brüder, die Neutronensterne, wenig beachtet. Dabei handelt es sich hier um ein weiteres Objekt der Superlative:
„Die Dichte innerhalb eines Neutronensterns ist so groß, dass er trotz einer Masse von etwa zwei Sonnen nur so groß ist wie Frankfurt!“
Es braucht gleich zwei von diesen außergewöhnlichen astronomischen Objekten, um schwere Elemente entstehen zu lassen – und sie müssen kollidieren. Wenn zwei Neutronensterne mit ihren gewaltigen Massen zusammenstoßen, kommt es zu einer sogenannten Kilonova, ein Phänomen, das erst 2017 durch die Messung von Gravitationswellen nachgewiesen wurde. Es wird davon ausgegangen, dass bei dieser Verschmelzung ein Zustand ähnlich dem in den ersten Sekunden nach dem Urknall herrscht, das sogenannte Quark-Gluon-Plasma. Quarks und Gluonen sind die elementaren Bestandteile von Atomkernen und somit Bausteine eines jeden Elements. Nur unter solch extremen Bedingungen wird ihre Anziehung aufgebrochen und die Entstehung schwerer Elemente erst möglich.
Die Wissenschaftler*innen des Clusterprojekts erforschen auf verschiedenen Wegen die Prozesse in diesen extremen Zuständen von Materie, wie schwere Elemente entstehen können und wie sich diese komplexen Interaktionen messen und von der Erde aus beobachten lassen. Während an den Teilchenbeschleunigern in Darmstadt auf mikroskopischer Ebene experimentiert wird, nähert man sich dem Problem an der Goethe-Uni von theoretischer Seite. Dabei spielen Open Science und Open Access, also die freie Zugänglichkeit von Daten und Ergebnissen, eine große Rolle: »Wir produzieren im Labor Daten auf ganz anderen Skalen als beispielsweise Astrophysikerinnen und Astrophysiker,« sagt Arbeitsgruppenleiterin Prof. Hannah Elfner. »Durch Open Science wird eine produktive interdisziplinäre Zusammenarbeit überhaupt erst möglich.«
»Wir befassen uns hier mit sehr komplexen wissenschaftlichen Fragen, die keine Einzelperson oder meine Arbeitsgruppe allein beantworten könnte, nicht ohne ein paar Jahrhunderte Zeit zu haben. Wir brauchen hier ein sehr großes Team.«, erklärt Luciano Rezzolla. So errechnet sein Team mithilfe von Supercomputern komplexe Modelle und Simulationen, die unerlässlich für die Interpretation astronomischer Beobachtungen sind. Basierend auf Einsteins Allgemeiner Relativitätstheorie können so Schwarze Löcher, Neutronensterne und ihre gewaltigen Interaktionen beschrieben und erklärt werden.
Die Arbeitsgruppe um Co-Sprecher Prof. Norbert Pietralla von der Technischen Universität Darmstadt holt hingegen am Elektronenbeschleuniger »S-DALINAC« das Universum direkt ins Labor und kann mit dem weltweit einzigartigen Energierückgewinnungsmodus Teilchen hocheffizient beschleunigen. Dabei drehen die Elektronen mehrere Runden durch den Hauptbeschleuniger, was erhebliche Mengen Energie einspart. Bei nahezu Lichtgeschwindigkeit können so die Wechselwirkungen bei der Entstehung neuer Elemente untersucht werden.
(pma)

Nachgefragt bei...
Luciano Rezzolla
Welches Problem wollen Sie im Clusterprojekt ELEMENTS lösen?
Bei ELEMENTS wollen wir verstehen, wie schwere Elemente, wie etwa Gold, im Universum entstanden sind. Überall finden wir Gold, aber es kommt weder von diesem Planeten noch aus Sternen, die sehr wenig schwere Elemente produzieren. Es muss also woanders entstanden sein. Deshalb betreiben wir Grundlagenforschung.
Warum ist das Thema wichtig für Sie?
Wenn man sich vorstellt, wie zwei Neutronensterne verschmelzen und dabei ein Schwarzes Loch produzieren, denkt man einfach nur »wow!«. Das Thema wird unser Leben nicht unmittelbar verändern. Aber es ist so ein besonderes Phänomen, das es zu erforschen lohnt.
Was sind Etappenziele?
Ein erster Meilenstein wäre die Erkenntnis, wie viel Masse verloren geht, wenn zwei Neutronensterne kollidieren. Sind es 0,1 Prozent oder 1 Prozent einer Sonnenmasse? Wir können damit beginnen, diese Frage zu beantworten, indem wir Simulationen berechnen. Danach können wir hoffentlich verstehen, wie diese verlorene Masse Gold und andere schwere Elemente produziert.
Welche Hürden liegen auf dem Weg?
Wir befassen uns hier mit sehr komplexen wissenschaftlichen Fragen, die nicht eine einzelne Person oder meine Arbeitsgruppe allein beantworten könnte, zumindest nicht ohne ein paar Jahrhunderte Zeit zu haben. Solche Fragen können nur sehr viele Wissenschaftler*innen gemeinsam beantworten.
Wie gehen Sie mit Misserfolgen um?
In der Wissenschaft sind Misserfolge die Normalität, nicht die Erfolge. Jedes Mal, wenn wir einen kleinen Schritt vorwärtskommen, liegt das daran, dass wir vorher mindestens dreimal hingefallen sind. Das rate ich auch meinen Studierenden: sich nicht zu sehr aufzuregen, wenn etwas schiefläuft, es nicht persönlich zu nehmen und einfach durchzuhalten. So schaffe ich das. Ich gebe einfach niemals auf.
Prof. Dr. Luziano Rezzolla ist Leiter der Arbeitsgruppe »Relativistische Astrophysik (RelAstro)« am Fachbereich Physik und, gemeinsam mit Prof. Dr. Dr. h.c.mult. Norbert Pietralla von der Technischen Universität Darmstadt, Sprecher des Clusterprojekts ELEMENTS.
Langfassung des Interviews:
Kurzfassung des Interviews:

Beim Lehrprojekt EXPLORE lernen Studierende, in internationalen Teams zu forschen.
Laura Sagunski, Leiterin einer Forschungsgruppe beim Clusterprojekt ELEMENTS, hat gemeinsam mit der York University in Toronto (Kanada) das innovative, internationale Lehrprojekt »EXPLORE« ins Leben gerufen. Bei EXPLORE (»Experiential Learning Opportunity through Research and Exchange«) lernen Studierende, in internationalen Teams zu forschen. Die Professorin am Institut für Theoretische Physik gibt damit eine Erfahrung weiter, die sie während ihrer wissenschaftlichen Laufbahn geprägt hat.
»Ich habe immer wieder festgestellt, dass die Zusammenarbeit in heterogenen Teams kreativer, innovativer und erfolgreicher ist. Sie bereichert nicht nur fachlich, sondern auch persönlich. Die Vielfalt und Internationalität innerhalb von ELEMENTS sehe ich deshalb als großes Potenzial, das ich gern an den wissenschaftlichen Nachwuchs weitergeben möchte.
Bei »EXPLORE« arbeiten deutsche und kanadische Studierende in selbstorganisierten Teams an einem Forschungsprojekt zu einer aktuellen physikalischen Fragestellung. Ziel des Projekts ist es, den Studierenden nicht nur spannende Fachkenntnisse zu vermitteln. Sie sollen auch die moderne Forschungspraxis in einem internationalen Team kennenlernen – und ihre Kompetenzen im Bereich der interkulturellen Kommunikation und der wissenschaftlichen Zusammenarbeit stärken. Moderne Forschung ist Teamarbeit!«

Laura Sagunski
»Die Vielfalt und Internationalität ist ein großes Potenzial«
Mathematiker sind einsame Denker. Von wegen! Der neue Sonderforschungsbereich der Mathematik versammelt verschiedene mathematische Disziplinen.
Wie Mathematiker*innen forschen? „Oft arbeiten wir ganz traditionell mit Papier und Kreidetafeln“, erzählt der Mathematiker Professor Jakob Stix. »Was wir aber in jedem Fall brauchen, ist ein Aufenthaltsraum mit einer guten Espresso-Maschine«. Denn für die Arbeit sei es enorm hilfreich, im kleinen Kreis anderen zu erzählen, woran man gerade arbeite. Gibt jemand mit einer anderen Expertise sein Feedback, habe man wieder für drei Tage Stoff zum Nachdenken. »Die Kommunikation ist auch in der Mathematik ein zentraler Punkt; das wird oft vergessen«, sagt der Sprecher des Sonderforschungsbereichs (SFB) Transregio (TRR) GAUS.
Die räumliche Konzentration von Experten in Geometrie und Arithmetik ist ungewöhnlich hoch in der strategischen Allianz der Rhein-Main-Universitäten (RMU) Frankfurt, Darmstadt und Mainz sowie der Universität Heidelberg. Das war für die Gründung des SFBs ausschlaggebend, zumal einige der Principle Investigators (PI) bereits in einer DFG-Forschergruppe und einem LOEWE-Schwerpunkt zusammengearbeitet haben. Für die Mathematik ist die Kooperation in größeren Gruppen eine neuere Entwicklung. Jahrelang trugen mathematische Publikationen in der Regel nur den Namen eines Autors. Heute sind es meist Tandems, manchmal auch drei oder vier Autoren. GAUS fördert diese Tendenz: Der SFB bringt Vertreter*innen verschiedener mathematischer Disziplinen zusammen, die sich mit ihren spezifischen Ansätzen, Werkzeugen und Erkenntnissen gegenseitig bereichern. Das mache die Arbeit abwechslungsreich und spannend, erzählt Stix.
Ein zentrales Forschungsthema von GAUS ist die Uniformisierung. Darunter versteht man Verfahren, die komplexe geometrische Strukturen in einfache überführen. »Bildlich gesprochen faltet man komplexe Strukturen bei der Uniformisierung auseinander«, erklärt Jakob Stix. Ein einfaches Beispiel ist das Spielzeug Slinky, eine Metallspirale, die sich in Purzelbäumen die Treppe hinunterbewegt. Von oben gesehen hat sie die Geometrie eines Kreises. Die Komplexität des Kreises besteht darin, dass man nach jeder Umrundung wieder zum Ausgangspunkt zurückkehrt. Markiert man die Ausgangspunkte auf jeder Etage und zieht die Spirale dann zu einem langen Draht auseinander, entsteht eine Linie, die in gleichmäßigen Abständen gepunktet ist. »So wird die ursprüngliche Komplexität des Kreises nach der Uniformisierung, das heißt dem geometrischen ‚Auseinanderfalten‘ in eine Gerade, und durch Symmetrien, also Translationen, des einfacheren Raums beschrieben: Die Punkte auf der Geraden bezeugen die Herkunft als Uniformisierung des Kreises«, erklärt Stix.
Ob der niederländische Zeichner M. C. Escher etwas von Uniformisierung geahnt hat, als er das Bild eines Kreises mit gebogenen Linien und Fischen malte? Es lässt sich jedenfalls so interpretieren, als habe er ein kompliziertes geometrisches Objekt auseinandergefaltet. Die sich wiederholenden Elemente sind hier Vierecke und Dreiecke, die zum Rand hin immer kleiner und verzerrter werden – ein Artefakt der Darstellung eines hyperbolisch gekrümmten Raumes auf dem flachen Zeichenpapier. Das geometrische Objekt, das dem Kreis als Draufsicht der Spirale beim Slinky entspricht, kann man sich nur noch schwer vorstellen. Es entsteht, indem man das Muster zerschneidet, von den sich wiederholenden Puzzlestücken (das zentrale Viereck und zwei angrenzende Dreiecke) nur jeweils eines behält und dieses an sich entsprechenden Kanten zusammenklebt. Dies entspricht einer Windung der Spirale. Um das Muster in Eschers Bild zu konstruieren, fügt man weitere benachbarte Vierecke und Dreiecke zusammen und hinzu, bis man die ganze Kreisscheibe bedeckt hat.

Die komplexe Figur aus Dreiecken illustriert ein zentrales Forschungsthema von GAUS: Wie versteht man komplexe geometrische Strukturen? Die Methode der Wahl ist die Uniformisierung, also ein Verfahren, das komplexe geometrische Strukturen in einfache mit vielen Symmetrien überführen kann.
Das Verlegen eines periodischen Parkettmusters in einer unendlichen Ebene, wie in vielen Bildern von Escher, ist ein weiteres Beispiel einer Uniformisierung, diesmal derjenigen eines Donuts. »Das Schöne ist, dass die uniformisierten Objekte viele Symmetrien tragen«, findet Professor Timo Richarz von der TU Darmstadt, GAUS-PI und als exzellenter Nachwuchswissenschaftler mit einem ERC-starting grant ausgestattet. An jedem der Schnittpunkte der Halbkreise auf dem Kreis, wo je drei Vierecke und drei Dreiecke zusammentreffen, kann man das ganze Bild drehen.
Eine weitere vom Sonderforschungsbereich genutzte Brücke zwischen Geometrie und Arithmetik basiert auf einem Konzept von Alexander Grothendieck aus den 1960er Jahren. »Es hat die Mathematik damals revolutioniert, davon leben wir heute noch«, sagt GAUS-PI Dr. Katharina Hübner von der Universität Heidelberg. Ein Beispiel dieses Konzepts fasst die ganzen Zahlen als Funktion auf der Menge der Primzahlen auf. So hat die Zahl 17 an der Stelle 2 den Wert »ungerade«, an der Stelle 3 den Wert 2 (denn 17 lässt bei Division durch 3 den Rest 2), an der Stelle 5 ebenfalls den Wert 2 (denn 17 lässt bei Division durch 5 den Rest 2) usw. Bei der 17 hat die 17 als Funktion eine Nullstelle. So entstehen neue Beziehungen zwischen den Zahlen: Als Funktionen haben so die 17 und die 101 denselben Wert bei 3.
Ein solches Konzept von ganzen Zahlen als Funktionen erlaubt die Übertragung der Intuition des geometrischen Funktionenbegriffs (man denke an Funktionsgrafen oder Nullstellen) in die Arithmetik der Zahlen. »Das ist das Einmaleins der arithmetischen Geometrie«, erklärt Stix. »Wir machen dazu Grundlagenforschung, aber einer meiner Doktoranden arbeitet in seiner Freizeit daran, eine Kryptowährung zu entwickeln, die gegen Quantencomputer-Angriffe stabil sein soll. Dabei wendet er dieses Wissen an.«
„Wenn irgendwann einmal Aliens kommen, werden wir uns vermutlich mit ihnen in der Sprache der Mathematik unterhalten können.“
Jakob Stix
Jakob Stix betrachtet die Mathematik als eine Naturwissenschaft: »Mathematische Strukturen sind Ideen, die so grundsätzlich konzeptionell sind, dass sie auf jeden Fall in der Natur auftauchen. Deswegen sind wir auch der Meinung: Wenn irgendwann einmal Aliens kommen, werden wir uns vermutlich mit ihnen in der Sprache der Mathematik unterhalten können. Denn die Mathematik ist so universell, dass auch die Aliens sie entdeckt haben müssen.«
(ahv)
Jakob Stix, Mathematiker und Sprecher des neuen Sonderforschungsbereichs »Geometrie und Arithmetik uniformisierter Strukturen – GAUS«
GAUS fördert Frauen
- Konferenzserie »Women in …«; 2022 »Women in arithmetic geometry«
- Coaching für Nachwuchswissenschaftlerinnen durch erfahrene Kolleginnen
- Master-Stipendien sollen zur Hälfte an Frauen vergeben werden
- Ruth Moufang-Lecture: Aufstrebende und etablierte Mathematikerinnen präsentieren ihre Forschung und dienen als weibliche Vorbilder
SFB TRR 326 »Geometrie und Arithmetik uniformisierter Strukturen – GAUS«
Goethe-Universität Frankfurt
Partner: Technische Universität Darmstadt, Universität Heidelberg
Assoziierte Institutionen: Johannes Gutenberg-Universität Mainz, Westfälische Wilhelms-Universität Münster
Wenn Komplexes einfach wird

Nachgefragt bei...
Jakob Stix
Welches Problem wollen Sie besser verstehen?
Die Wechselwirkung zwischen Geometrie, also strukturierten raumartigen Objekten, und Arithmetik, also algebraischen Eigenschaften von Zahlen.
Was ist ein Etappenziel?
Damit mathematische Grundlagenforschung gedeihen kann, brauchen wir Freiräume und Ideenwerkstätten, damit die Gedanken aufblitzen und dann in kleineren Gruppen ausgearbeitet werden können. Die dafür günstigen Rahmenbedingungen zu schaffen, ist das wichtigste Etappenziel.
Was ist die größte Hürde?
Mathematik lebt auch von der Kommunikation. Bei dem Neubau, der in den nächsten Jahren am Campus Riedberg für den Fachbereich Mathematik entstehen wird, brauchen wir einen Ort, an dem der SFB-TRR GAUS gemeinsame Räumlichkeiten und »Freiräume« erhält.
Gibt es eine Erkenntnis, die Sie besonders geprägt hat und die Sie in dieses Projekt quasi als Rüstzeug »mitnehmen«?
Die Methode »la mer qui monte« von Grothendieck. Das heißt, den Dingen fundamental und konzeptionell auf den Grund gehen, damit das grundsätzliche Verständnis an Qualität gewinnt und sich die ursprünglichen Forschungsfragen leicht(er) beantworten lassen.
Wie gehen Sie mit Misserfolgen um?
Frustrationstoleranz lernt man in der mathematischen Forschung schnell. Von den vielen Ideen, die wir ausprobieren, funktionieren nur wenige so gut, dass wir begeistert sind und die Mathematik einen Schritt weitergekommen ist. Aber da wir viel mit Papier und Bleistift oder auch der guten alten Kreidetafel arbeiten, entsorgen wir Misserfolge mit dem Altpapier oder wischen die Tafel und starten dann mit neuen Ideen.
Wie feiern Sie Erfolge?
In der Gruppe mit einem Kaffee.
Prof. Dr. Jakob Stix ist Mathematiker und Sprecher des neuen Sonderforschungsbereichs »Geometrie und Arithmetik uniformisierter Strukturen – GAUS«.

Als Julia Sammet das Physik-Lernzentrum gründet, ist sie selbst Studentin. Inzwischen leitet die Doktorandin das Zentrum mit ihrem Team seit acht Jahren. Und erhält Preise für ihre Leistung.
Manche guten Dinge entstehen nebenbei, quasi absichtslos. Aber sie bringen etwas ins Rollen. Im Fall von Julia Sammet, die sich im Bachelor-Studium in der Fachschaft Physik engagiert, ist dies im Jahr 2013 eine kurze Nachricht in den Facebook-Gruppen ihrer Kommiliton*innen. »Hey Leute, ich bin morgen in Raum 02.428 und beantworte Fragen zu Übungen zur theoretischen Physik. Wer will, kann gern kommen.« Am folgenden Tag finden sich zwei Interessierte ein, in der nächsten Woche sind es ein paar mehr. Nach einigen Wochen hat sich herumgesprochen, dass es sich lohnt, dem Raum einen Besuch abzustatten: weil dort unter Anleitung Übungsaufgaben bearbeitet werden, die man allein kaum zu schaffen glaubt. Und mehr noch: weil man sich gemeinsam beim Verstehen hilft. Damals studiert Julia Sammet im dritten Semester Physik und legt – ohne es zu merken – den Grundstein zum Physik-Lernzentrum.
Überspringen wir die Jahre seit 2013, treffen wir auf ein Zentrum, das mit beachtlichen Zahlen aufwarten kann. Julia Sammet, die inzwischen am Fachbereich promoviert, hat Buch geführt: Aus anfänglich einem Übungstag sind fünf Tage pro Woche geworden, an denen im Präsenzarbeitsraum vier Stunden täglich bis zu vierzig Studierende von Peer-Tutoren betreut werden. Darunter sind Studierende der Physik ebenso wie der Geowissenschaften, Biophysik, Biochemie, Chemie, Pharmazie und Biowissenschaften. 1392 Besuche wurden während des Wintersemesters 2018/19 im Lernzentrum registriert, im online-geprägten Wintersemester 2020/21 waren es 939 Logins. Zur anfänglichen ehrenamtlichen Beratung sind nach einem Jahr Mittel des Fachbereichs für Hilfskräfte inzugekommen. Gemeinsam mit dem 2015 gegründeten Mathematikzentrum bewirbt sich der Fachbereich Physik 2017 erfolgreich auf ein Innovationsprojekt im »Starken Start ins Studium« und sichert damit die langfristige Finanzierung des Physik-Lernzentrums.
Dumme Fragen gibt es nicht
Das Lernzentrum, so belegen es die Zahlen, ist vom Campus Riedberg also nicht mehr wegzudenken. Doch das war nicht immer so. Sollte nicht besser – so war anfangs zu hören – die bereits existierende Tutorenbetreuung ausgebaut werden? Fördert ein Lernzentrum vielleicht eher die Wackelkandidaten, die das Studium ohnehin bald aufgeben? »Selbst wenn es so wäre«, kontert Professor Reinhard Dörner, Studiendekan des Fachbereichs Physik, »wäre das doch sehr positiv. Die Besten fördern kann jeder«. Für den Fachbereich, soviel steht für Dörner fest, füllt das niederschwellige Angebot des Lernzentrums eine Lücke. Und das hat der Fachbereich inzwischen sogar amtlich: Externe Gutachter haben bei einer Beurteilung des Physik-Studiengangs der Goethe-Universität die Qualität des Lernzentrums lobend erwähnt. Für Dörner leistet das Lernzentrum aber noch etwas Wesentliches für das Physikstudium. »Auch wenn man am Ende allein rechnen muss:
»Physikalische Probleme werden im Diskurs erarbeitet. Im Lernzentrum lernt man das.«
Professor Reinhard Dörner, Studiendekan des Fachbereichs Physik
Auch für Julia Sammet ergänzen sich die Angebote von obligatorischen Tutorien und freiwilligem Lernzentrum auf sinnvolle Weise – als ehemalige Fachbereichstutorin weiß sie, wovon sie spricht. Während in den Tutorien zu einer Vorlesung Lösungen der wöchentlichen Übungsaufgaben Thema sind, werden die Studierenden im Lernzentrum beim Lösen dieser Aufgaben begleitet: Wo hakt es? Hat jemand eine Idee? Im Lernzentrum können zudem die Themen für kreatives Grübeln frei gewählt werden. Dabei, das ist Julia Sammet besonders wichtig, sei keine Frage zu dumm, um nicht gestellt zu werden. Die Hilfskräfte des Lernzentrums müssen deshalb mit ihrem Wissen breit aufgestellt sein. Fünf studentische Hilfskräfte beschäftigt das Lernzentrum heute. Aus den Bewerbungen kann Julia Sammet sich die Jahrgangsbesten aussuchen – und diese prüft sie dann auf ihre Fähigkeit, geduldig, kreativ und – besonders wichtig – freundlich zu erklären. Im Vorstellungsgespräch übernimmt die Doktorandin die Rolle der fragenden Studentin, gemäß ihrer Devise: Dumme Fragen gibt es nicht. Die ausgewählten Hilfskräfte bleiben dann meist jahrelang. Wie Tutor Daniel Jampolski, der heute im achten Fachsemester studiert und das Lernzentrum vom zweiten Semester an »fast jeden Tag« besucht hat. »Man spart sich damit eine Menge Zeit«, erklärt er, denn »mit guten Denkanstößen« schaffe man die Übungsaufgaben natürlich schneller. Außerdem habe er im Lernzentrum immer Kommilitonen getroffen – befreundet sind sie bis heute.
Wer sich das Lernzentrum also als simple Hausaufgabenhilfe vorstellt, denkt zu kurz. Das Team versteht es als Zentrum, wo das Lernen gelernt werden soll. Oder noch größer gedacht: Bei dem gelernt werden soll, wie Forschen geht. Dabei hat Julia Sammet sich an der Frage orientiert: Was würde mir selbst helfen, zu verstehen? Von ihrer pädagogischen Erfahrung profitieren inzwischen auch die Teilnehmer*innen der naturwissenschaftlichen Vorkurse auf dem Riedberg, die Julia Sammet mit ihrem Team ebenfalls leitet: Pro Semester werden um die 280 Abiturientinnen und Abiturienten vor dem Start an der Goethe-Uni mit physikalischem Basiswissen vertraut gemacht.
Hocheffektiv und erfolgreich sind Lernangebote des Physik-Lernzentrums nicht zuletzt auch, weil hinter dem Konzept viel Arbeit steckt. Neben Lehrvideos gibt es Übungen angepasst an alle Teilnehmenden – mit Physik-Vorkenntnissen und ohne. Von Anfang an hat Sammet gemeinsam mit dem EdTech-Start-up StudyCore auch eine spezielle Learn-Analytics-Plattform entwickelt, mit der die Studierenden unmittelbares Feedback zu ihrem Lernstatus erhalten. Und sie scheut keine Mühe und Versuchsaufstellung, um auch mit praktischen Experimenten Verständnisprozesse in Gang zu bringen. Um etwa den Unterschied zwischen inelastischen und elastischen Stößen zu erklären, hat sie mit ihrem Team Züge aufeinanderprallen lassen und bei Versuchen mit normaler Knete und Springknete gearbeitet. Dabei sollte ein Student Springknete im Wurf an eine Wand heften. Als diese wiederholt den Kursteilnehmenden um die Ohren flog, hatten nicht nur alle etwas über den Unterschied von inelastischen und elastischen Stößen verstanden, sondern auch eine Menge Spaß.
Es überrascht nicht, dass auch der Ausbruch der Pandemie das Lernzentrum nur für kürzeste Zeit ausgebremst hat. Professoren halfen mit dem nötigen Equipment aus, damit der Vorkurs rechtzeitig online starten konnte. Ob im Vorkurs oder Lernzentrum – die Studierenden spüren die Impulse an ihren eigenen Erfolgen. Und sie setzen sich deshalb zunehmend dafür ein, das Zentrum und seine Leiterin bekannt zu machen – indem sie etwa erfolgreich ihr Vorschlagsrecht für Preise nutzten. 2019 wurde die damals 26-Jährige mit dem eigens für sie eingerichteten Sonderpreis »Auszeichnung für besonderes Engagement von Studierenden im Bereich der Lehre« prämiert. 2020 erhielt sie den 1. Preis des »1822-Universitätspreis für exzellente Lehre« der Goethe-Universität und der Stiftung der Frankfurter Sparkasse, der damit erstmals an den Fachbereich Physik ging. 2021 dann erhielt sie vom Institut für Theoretische Physik der Goethe-Universität den »Niko-Claus-Preis für gute Lehre« der Walter Greiner Gesellschaft zur Förderung der physikalischen Grundlagenforschung e.V.
Die Preise haben etwas verändert. Nicht nur das Lernzentrum wird geschätzt, der Fokus richtet sich auch auf die Person, ohne die es das Zentrum gar nicht gäbe. Julia Sammet will nun ihre Promotion abschließen – und kann sich gut vorstellen, dem Lernzentrum verbunden zu bleiben. Weil man dort, sagt sie, Forschen und Lehren so sinnvoll verbinden kann.
Unser Forschungsprofil: Raum für gute Antworten
Mit sechs Profilbereichen will die Goethe-Universität ihre Kompetenzen stärker bündeln.

