The profile area Space, Time & Matter explores the physical and mathematical foundations of the natural sciences in six research areas: from the elementary building blocks of matter, to the interaction of the building blocks in solids, artificially producible quantum materials, the atmosphere and Earth’s interior, planets and neutron stars. This requires mathematically precise models and efficient algorithms for the numerical exploration.

Extreme States
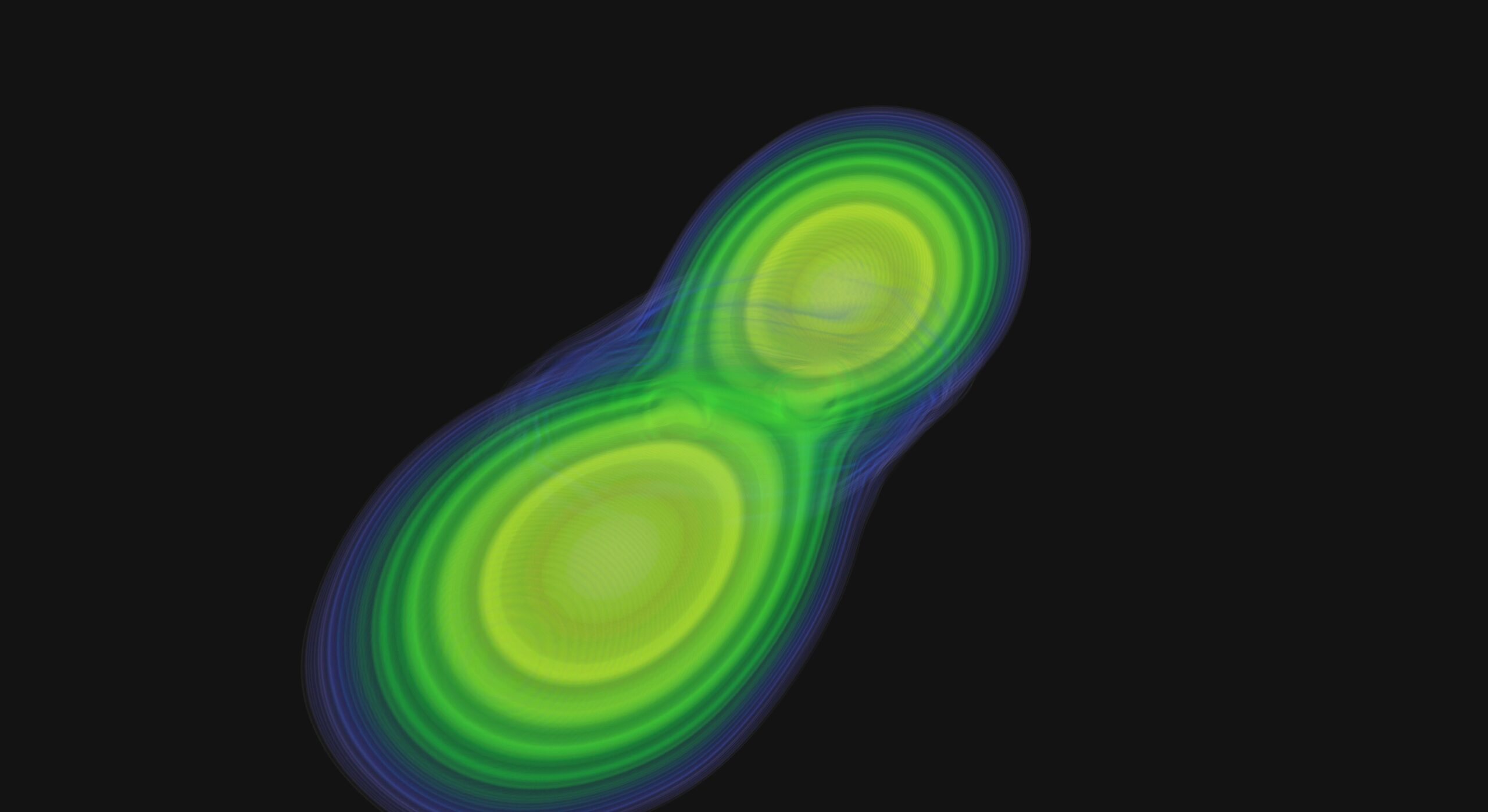
In the ELEMENTS cluster project, around a hundred particle physicists and astrophysicists have joined forces with the goal of understanding how heavy elements are produced in our universe through the merger of neutron star binaries.
Our universe is full of extremes: incredibly massive and compact objects collide at an unimaginable distance to release the tiniest particles. It is precisely these extreme phenomena that are a central topic in the ELEMENTS research project (Exploring the Universe from Microscopic to Macroscopic Scales). Theorists and experimenters are working together on the question of how heavy elements, for example gold and platinum, form in the universe. “Our research is fundamental – because gold is all around us but did not originate on our planet,” explains Professor Luciano Rezzolla from the Institute for Theoretical Physics at Goethe University Frankfurt, speaker for the ELEMENTS project. “But it doesn’t come from the stars either, which produce very few heavy elements.” What the some 100-strong team from Goethe University Frankfurt, TU Darmstadt, the University of Giessen and the GSI Helmholtz Centre for Heavy Ion Research therefore in principle wants to know is: Where does our gold come from?
This requires a few ingredients and a lot of time. At the end of its long life, a star collapses under its own gravity and explodes as a supernova. Gas, dust and lots of energy are hurled into the surrounding space. Later, these remnants are visible as nebulae with fascinating shapes and colours. Depending on how massive the star originally was, a black hole (very massive star) or a neutron star (not very massive) forms. While black holes are widely known, their little brothers, neutron stars, receive little attention. Yet this is another superlative:
"The density within a neutron star is so great that – despite a mass of about two suns– it is only as big as Frankfurt!“
It takes two of these extraordinary astronomical objects to create heavy elements – and they have to collide. When two neutron stars with their enormous masses collide, they emit very intense gravitational waves and form an object whose density and temperature are similar to those in the first seconds after the Big Bang, possibly even creating a so-called quark-gluon plasma. Quarks and gluons are the elementary components of atomic nuclei and thus the building blocks of every element. In addition to gravitational waves, the colliding stars also expel a tiny amount of their mass and while this is less than 1% of the total mass, it is what later will produce heavy elements through a complex nucleosynthesis. The transformation of the expelled matter also leads to a very special type of light, called kilonova, which has been observed in 2017 together with the first gravitational waves from merging neutron stars (GW170817).
The researchers in the cluster project are examining in different ways the processes in these extreme states of matter, how heavy elements can form and how these complex interactions can be measured and observed from Earth. While experiments are being conducted on a microscopic level at particle accelerators such as the one at GSI, a lot of work is also done on the theoretical side, especially at Goethe University Frankfurt. Open science and open access, that is, freely accessible data and results, play an important role here: “In the laboratory, we produce data on completely different scales than astrophysicists, for example,” says research group leader Hannah Elfner. “Open science is what makes productive interdisciplinary collaboration possible in the first place.”
With the help of supercomputers, Luciano Rezzolla’s team calculates complex models and simulations that are indispensable for interpreting astronomical observations. In this way, black holes, neutron stars and their enormous interactions can be described and explained, using Einstein’s General Theory of Relativity as the basis. “We’re dealing here with very complex scientific questions that no one person or my research group alone could answer, not without having a few centuries of time to do so. A large team and a team spirit is essential in this research” explains Luciano Rezzolla.
The research group led by co-speaker Professor Norbert Pietralla from the Technical University of Darmstadt, on the other hand, brings the universe directly into the laboratory at the “S-DALINAC” electron accelerator and can accelerate electrons very efficiently by means of the energy recovery mode, which is unique worldwide. In this process, the electrons circulate several times through the main accelerator, which saves considerable amounts of energy. This makes it possible to study the interactions in the formation of new elements at almost the speed of light.
(pma)

We asked...
Luciano Rezzolla
Which problem do you want to solve in the ELEMENTS research project?
Through ELEMENTS, we want to understand how heavy elements, such as gold, formed in our universe. Gold is all around us, but it did not originate on our planet, nor did it come from the stars, which produce very few heavy elements. That means it must have originated somewhere else, and what is fascinating is that it appears that gold is actually produced in a very extreme process: the collision of two neutron stars! Realising that the answer to simple questions hides a fascinating scenario is what drives us to conduct fundamental research.
Why is this topic important for you?
When you imagine how two neutron stars merge to produce a black hole, you just think “Wow! It’s amazing what can happen in nature”. Although discovering the details of how this process takes place will not have an immediate impact on our lives, it is a complex and extraordinary phenomenon that simply begs to be explored.
What is your milestone?
A first milestone would be to know how much mass is lost when two neutron stars collide. Is it 0.1 percent or 1 percent of a solar mass? We can begin to answer this question by performing complex numerical simulations that describe this process. This is only the first step, but an important one towards understanding how this lost mass can then produce gold and other heavy elements.
Which obstacles are there along the way?
The largest obstacle is complexity. We are dealing here with an extremely complex process where numerous microphysical and macrophysical questions need to be addressed. This is something that no single person or my research group alone could answer, at least not without having a few centuries of time to do so. Such questions can only be answered by a very large team of scientists working together.
How do you deal with failure?
In science, failure – and not success! – is the norm. Each time we take a small step forward, it is because we fell down at least three times before. I advise my students to do the same: Don’t get too upset when something goes wrong, don’t take it personally and just persevere. Success is waiting at the next attempt.
Professor Luciano Rezzolla is head of the research group “Relativistic Astrophysics” at the Faculty of Physics and spokesperson of the ELEMENTS research project, together with Professor Norbert Pietralla from the Technical University of Darmstadt.
Langfassung des Interviews:
Kurzfassung des Interviews:

In the EXPLORE teaching project, students learn how to conduct research in international teams.
Together with York University in Toronto (Canada), Laura Sagunski, professor at the Institute for Theoretical Physics and head of a research group in the ELEMENTS project, has launched the innovative, international teaching project “EXPLORE”. Within EXPLORE (“Experiential Learning Opportunity through Research and Exchange”), students learn to conduct research in international teams. Laura Sagunski is thus passing on the experience that has shaped her during her academic career.
“I’ve repeatedly found that collaboration in heterogeneous teams is more creative, more innovative and more successful. It’s not only professionally but also personally enriching. That’s why I believe that diversity and internationality within ELEMENTS offer great potential, which I would like to pass on to early career researchers.
In "EXPLORE", German and Canadian students work in self-organized teams on a research project on a current physics issue. The aim of the project is not only to provide the students with exciting technical knowledge. They should also get to know modern research practice in an international team – and strengthen their skills in intercultural communication and scientific cooperation. Modern research is teamwork!”

Laura Sagunski
“Diversity and internationality offer great potential”
Are mathematicians really lonely thinkers? In bringing together various mathematical disciplines, the new Collaborative Research Centre in the field of mathematics suggests otherwise.
How do mathematicians conduct research? “We often work quite traditionally with paper and blackboards,” says mathematician Professor Jakob Stix. “But what we in any case need is a common room with a good espresso machine because communication is at the heart of mathematics too; that is often forgotten,” says Stix, speaker for the GAUS project, a Collaborative Research Centre (CRC)/Transregio (TRR).
The concentration of geometry and arithmetic experts in one place is unusually high in the strategic alliance of the Rhine-Main Universities (RMU), Frankfurt, Darmstadt and Mainz, together with the University of Heidelberg. That was the deciding factor for setting up the CRC, the more so as some of the principal investigators (PIs) have already worked together in a Research Unit of the German Research Foundation and a LOEWE Priority Programme. For mathematics, collaboration in larger groups is a recent development. For years, mathematical publications usually bore the name of only one author. Today, it is mostly tandems, sometimes even three or four authors. GAUS follows this trend: the CRC brings together representatives from various different mathematical disciplines who mutually enrich each other with their specific approaches, instruments and insights. This makes the work varied and exciting, says Stix.
One of the central research topics in the GAUS project is uniformisation. Understood by this are methods that convert complex geometric structures into simple ones. “Figuratively speaking, in uniformisation, complex structures are unfolded,” Jakob Stix explains. A simple example is Slinky, the toy in the shape of a metal spiral that somersaults downstairs. Seen from above, it has the geometry of a circle. The complexity of the circle lies in the fact that you return to the starting point after each full rotation. If you mark the starting points on each loop of the spiral and then pull the spiral apart into a long wire, the result is a line that is dotted at equidistant intervals. “Thus, the original complexity of the circle is described after uniformisation (the geometric ‘unfolding’ into a straight line) by symmetries (translations) of a simpler space: the dots on the straight line testify to the origin as a uniformisation of the circle,” explains Stix.
Whether Dutch draughtsman M. C. Escher had some inkling of uniformisation when he produced his woodcut of a circle with curved lines and fish? In any case, it can be interpreted as if he had unfolded a complicated geometric object. The recurring elements here are squares and triangles that become smaller and smaller and more distorted towards the edge – an artefact that represents a hyperbolically curved space on flat drawing paper. It is difficult to imagine the geometric object that corresponds to the circle as the top view of Slinky’s spiral. It is produced by cutting up the pattern, keeping only one of each of the recurring puzzle pieces (the square in the middle and two adjacent triangles) and gluing them together at their corresponding edges. This equates to one coil of the spiral. To build the pattern in Escher’s woodcut, you join further adjacent squares and triangles together and add them until you have covered the whole circle.

Die komplexe Figur aus Dreiecken illustriert ein zentrales Forschungsthema von GAUS: Wie versteht man komplexe geometrische Strukturen? Die Methode der Wahl ist die Uniformisierung, also ein Verfahren, das komplexe geometrische Strukturen in einfache mit vielen Symmetrien überführen kann.
Laying a periodic parquet pattern over an infinite plane, as in many of Escher’s works, is another example of uniformisation, this time that of a doughnut. “The beauty of it is that uniformised objects contain many symmetries,” says Professor Timo Richarz of TU Darmstadt, principal investigator for the GAUS project and, as an excellent early career researcher, recipient of an ERC Starting Grant. At each of the intersections of the semicircles on the circle, where three squares and three triangles each meet, you can rotate the whole picture.
Another connection between geometry and arithmetic explored by the Collaborative Research Centre is based on a concept by Alexander Grothendieck from the 1960s. “It revolutionised mathematics back then, and we still make use of it today,” says Dr Katharina Hübner, principal investigator for the GAUS project at the University of Heidelberg. One example of this concept is the consideration of whole numbers as a function of the set of prime numbers. For example, the number 17 has the value “odd” at the prime number 2, the value 2 at the prime number 3 (because 17 leaves the remainder 2 when divided by 3), the value 2 at the prime number 5 as well (because 17 leaves the remainder 2 when divided by 5), and so on. At the prime number 17, the value of the function 17 is zero. This creates new relationships between the numbers: as functions, 17 and 101 have the same value at the prime number 3.
Such a concept of whole numbers as functions makes it possible to transfer the intuition of the geometric concept of functions to the arithmetic of numbers. “This is the basics of arithmetic geometry,” explains Stix. “We do fundamental research on this, but one of my doctoral students is using this knowledge in his spare time to develop a cryptocurrency that should be stable against attacks from quantum computers.”
“If aliens arrive someday, we’ll probably be able to converse with them in the language of mathematics.”
Jakob Stix
Jakob Stix sees mathematics as a natural science: “Mathematical structures are ideas that are so fundamentally conceptual that they by all means occur in nature. That’s why we also believe that if aliens arrive someday, we’ll probably be able to converse with them in the language of mathematics. Because mathematics is so universal that aliens must have discovered it too.”
(ahv)
Jakob Stix, mathematician and speaker of the new Collaborative Research Center "Geometry and Arithmetic of Uniformized Structures - GAUS"
GAUS support for women
- Conference series “Women in …”; 2022 “Women in Arithmetic Geometry”
- Coaching for young researchers by experienced female colleagues
- Half of all Master’s scholarships are to be awarded to women
- Ruth Moufang Lecture: Aspiring and established female mathematicians present their research and function as female role models
CRC TRR 326“Geometry and Arithmetic of Uniformised Structures – GAUS”
Goethe University Frankfurt
Partners:Technical University of Darmstadt, University of Heidelberg
Associated institutions:Johannes Gutenberg University Mainz, University of Münster
When complex is made simple

We asked...
Jakob Stix
Which problem do you want to understand better?
The connection between geometry, that is, structured, space-like objects, and arithmetic, that is, algebraic properties of numbers.
What is your milestone?
For basic mathematics research to flourish, we need free space and brainstorming workshops to spark ideas that we can then work on in smaller groups. Creating favourable conditions for this is the most important milestone.
What is the biggest obstacle?
Mathematics too lives from communication. In the new building to be constructed in the next few years on Riedberg Campus for the Faculty of Computer Science and Mathematics, we need an environment where the CRC-TRR GAUS will have both a shared common room as well as spaces to reflect on our ideas individually.
Have you discovered anything that has particularly influenced you?
Grothendieck’s “rising sea” approach. That means getting to the fundamental and conceptual bottom of things so that our basic understanding gains in quality and the original research questions can be answered (more) easily.
How do you deal with failure?
Tolerating frustration is something you learn quickly in mathematics research. Of the many ideas we try out, only a few work so well that we’re really thrilled and mathematics takes a step forward. But as we work a lot with paper and pencil or even the good old blackboard, we throw our failures away with the waste paper or wipe the board clean and start again with new ideas.
How do you celebrate success?
Together, with a cup of coffee.
Professor Jakob Stix is a mathematician and spokesperson for the new Collaborative Research Centre “Geometry and Arithmetic of Uniformised Structures – GAUS”.

When Julia Sammet set up the Physics Learning Centre, she was still a student herself. Now a doctoral researcher, she has headed the centre for eight years, together with her team. And received prizes for her achievements.
Some good things happen by the by, as if unintentionally. But they get the ball rolling. In the case of Julia Sammet, who was involved in the Physics Student Council during her Bachelor’s studies, it was a short message in her fellow students’ Facebook groups in 2013. “Hey everyone, I’ll be in room 02.428 tomorrow answering questions about the theoretical physics exercises. Feel free to come along.” The following day, two people showed up, and the next week a few more. After a few weeks, word had got round that it was worth going because there, under guidance, you could work on exercises that you could scarcely solve alone. And even more so because people put their heads together to help each other understand. At that time, Julia Sammet was studying physics in her third semester and – without realising it – laying the foundation for the Physics Learning Centre.
If we skip the years since 2013, we find a centre that can boast impressive figures. Julia Sammet, who is now undertaking her doctoral degree at the faculty, has kept records: what was initially one practice day per week has grown into five, on which up to forty students are supervised by peer tutors for four hours a day in the classroom. Among them are physics students as well as geoscience, biophysics, biochemistry, chemistry, pharmacy and life science students. 1,392 visits to the learning centre were registered in the 2018/19 winter semester, and 939 logins during the mostly online 2020/21 winter semester. After a year, what was initially a service run by volunteers received funding from the faculty for assistants. Together with the Mathematics Centre set up in 2015, the Faculty of Physics successfully applied for an innovation project in the “Starker Start ins Studium” initiative (“Strong Start to Studies”) in 2017, thus securing long-term finance for the Physics Learning Centre.
There is no such thing as a stupid question
Riedberg Campus is now unimaginable without the learning centre, as the figures corroborate. But that was not always the case. Wouldn’t it be better – it was heard initially – to expand existing tutoring? Would a learning centre perhaps be more likely to encourage students with a question mark next to their names, who would soon drop out anyway? “Even if that were the case,” counters Professor Reinhard Dörner, Dean of Studies at the Faculty of Physics, “that would in fact be very positive. Supporting the best is easy.” For the faculty, Dörner is certain, the learning centre’s low-threshold offer fills a gap. And the faculty meanwhile even has official proof of this: in an evaluation of the physics degree programme at Goethe University Frankfurt, external experts praised the quality of the learning centre. For Dörner, however, the learning centre accomplishes something else which is essential for physics studies. “Even if at the end of the day you’re obliged to do the maths on your own, physics problems are solved through discourse. And that’s what you learn at the learning centre.”
“Physics problems are solved through discourse. That’s what you learn at the Learning Centre.”
Professor Reinhard Dörner, Dean of Studies, Faculty of Physics
For Julia Sammet, too, compulsory tutorials and the voluntary learning centre complement each other in an expedient way – as a former tutor at the faculty, she knows what she’s talking about. Whereas the lecture tutorials concentrate on finding solutions to the weekly exercises, the learning centre helps students with how to solve exercises by learning from each other: Where is the problem? Does anyone have any ideas? In addition, in the learning centre, students are also free to choose their own topics on which they then ponder creatively. For Julia Sammet, it is particularly important to emphasise that no question is too stupid to be asked. The learning centre’s assistants must therefore have wide-ranging knowledge. Today, the learning centre employs five student assistants. Julia Sammet can choose the best of the year from among the applications – and she then tests the candidates on their ability to explain patiently, creatively and, most importantly, in a friendly way. In the interview, she assumes the role of the student asking the questions, according to her principle: There is no such thing as a stupid question. The assistants selected then usually stay for years. Like tutor Daniel Jampolski, a student who is now in his eighth semester and has visited the learning centre “almost every day” from his second semester onwards. “You save a whole lot of time,” he explains, because “with good input” you naturally get through the exercises faster. In addition, he says, he always met fellow students at the learning centre – they are still friends today.
Anyone imagining the learning centre as a simple service to help with homework is therefore thinking too narrowly. The team sees it as a centre for learning how to learn. Or, thinking on a greater scale, as a place to learn how to conduct research. Julia Sammet’s approach is based on the question: What would help me to understand? The participants in the preliminary science courses on Riedberg Campus, which Julia Sammet and her team also run, are meanwhile also benefiting from her didactics experience: each semester, around 280 school leavers become acquainted with basic physics before starting at Goethe University Frankfurt.
The learning opportunities offered by the Physics Learning Centre are highly effective and successful, not least because a lot of work is invested in the concept. In addition to teaching videos, there are exercises adapted to all participants – with and without prior physics knowledge. Right from the start, Sammet also developed a special learning analytics platform together with the edtech start-up StudyCore, which gives students immediate feedback on their learning status. And she leaves no stone unturned and goes out of her way to stimulate understanding processes through practical experiments. To explain the difference between inelastic and elastic collisions, for example, she and her team let trains crash together and conducted experiments with normal and bouncing putty: a student was asked to throw bouncing putty against a wall and make it stick. When it repeatedly whizzed past the course participants’ ears, not only had everyone understood something about the difference between inelastic and elastic collisions, but they had also had a lot of fun.
It is not surprising that even the outbreak of the pandemic was unable to slow down the learning centre for very long. Professors helped out with the necessary equipment so that the preliminary course could start online in time. Whether in the preliminary course or the learning centre, students are motivated by their own success. And they are therefore increasingly committed to making the centre and its director known – for example by making use of their right to propose awards. In 2019, Julia Sammet, then 26, was awarded the special prize “Student Award for Special Commitment in Teaching”, which was introduced especially for her. In 2020, she received 1st prize of the “1822 University Prize for Excellent Teaching” of Goethe University Frankfurt and the foundation of Frankfurter Sparkasse, which thus went to the Faculty of Physics for the first time. In 2021, the Institute for Theoretical Physics of Goethe University Frankfurt awarded her the “Niko Claus Prize for Good Teaching” of the Walter Greiner Society for the Promotion of Physical Basic Research.
The prizes have changed a little. Not only is the learning centre greatly appreciated, but the focus is also on the person without whom the centre would not even exist. Julia Sammet now wants to complete her doctoral degree – and can well imagine remaining associated with the learning centre. Because there, she says, you can combine research and teaching in such a meaningful way.
Unser Forschungsprofil: Raum für gute Antworten
Mit sechs Profilbereichen will die Goethe-Universität ihre Kompetenzen stärker bündeln.

