Die Mutter der wissenschaftlichen Ordnungssysteme

Mathematik vom antiken Ägypten bis zur Coronapandemie

von Annette Imhausen

Mathematik begegnet uns jeden Tag und überall. Unser aller Alltag wird durch Zahlen, Maße und darauf aufbauende Strukturen grundlegend geordnet. So sind die Tage einer Woche in aufeinanderfolgende Einheiten von 24 Stunden geordnet. Wir erwarten, dass Geschäfte zu bestimmten Uhrzeiten öffnen (und schließen), ebenso wie wir auf pünktliches (also zu einer bestimmten Zeit) Abfahren und Ankommen von Bus oder Bahn zumindest hoffen. Was wir morgens anziehen, machen wir abhängig von der Information, wie heiß oder kalt es ist – einer Zahlenangabe in Grad Celsius. Kaufen, verarbeiten oder essen wir Lebensmittel, geschieht dies in bestimmten Mengen.

Zahlen und damit verbundene Maßsysteme, mit denen wir unseren Lebensraum ordnen, sind nicht erst in der modernen Welt allgegenwärtig. Sie lassen sich weit in die Geschichte zurückverfolgen. Die Verwendung von Zahlen und Maßsystemen zur Strukturierung von Ressourcen aller Art ist bereits aus dem antiken Ägypten und aus Mesopotamien zu belegen, wo sich im 4. Jahrtausend vor unserer Zeitrechnung Zahlen und Schriftzeichen entwickelt haben, und zwar im Zusammenhang mit der Herausbildung einer hierarchisierten Gesellschaft. Dabei ist, wie sich in Mesopotamien verfolgen lässt, die Erfindung der Schrift vermutlich erst durch die Entwicklung der Zahlen und Maße ausgelöst worden.

Zur Ordnung, aber auch zur Kontrolle von Ressourcen wurden dann mathematische Techniken entwickelt, die in Form von Aufgabensammlungen und deren Lösungen in Ägypten und Mesopotamien seit dem zweiten Jahrtausend vor unserer Zeitrechnung erhalten sind. Aus solchen Sammlungen lassen sich auch Informationen über die Menschen dieser Zeit und ihre Wertvorstellungen ableiten. So wird in einigen Aufgaben etwa die Zuteilung von Rationen behandelt, deren Menge aufgrund der gesellschaftlichen Stellung berechnet wird: Der Vorsteher bekommt ein Vielfaches der Menge des einfachen Arbeiters. Hier spiegelt sich die Idee einer als göttlich vorhergesehenen, gesellschaftlichen Ordnung (ägyptisch als Maat bezeichnet) wider, in der jeder seinen festen Platz hatte und diesem Platz entsprechend Verpflichtungen und Ansprüche ableiten konnte.

Euklid: einflussreich wie die Bibel

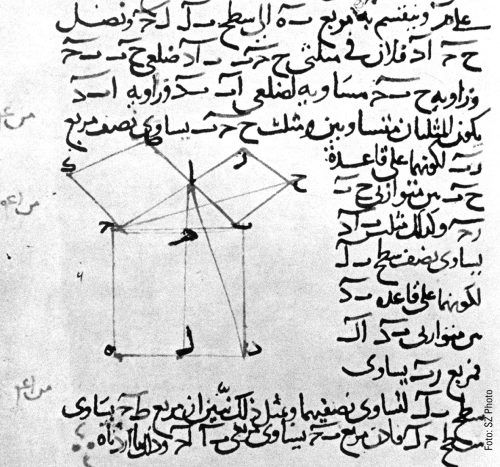
Eine weitere Entwicklung und auch ein neuer Anspruch an eine mathematische Ordnung finden sich in den mathematischen Texten des antiken Griechenlands. Die 13 Bücher der Elemente von Euklid (3.  Jahrhundert vor unserer Zeit) sind die früheste erhaltene axiomatisch-deduktiv aufgebaute Sammlung mathematischen Wissens. »Axiomatisch-deduktiv« beschreibt die Struktur des mathematischen Werks: Nachdem Euklid im ersten Buch grundsätzliche Objekte (wie zum Beispiel Punkt, Gerade und Kreis) und Operationen (wie zum Beispiel das Verbinden zweier Punkte durch eine Gerade) der Geometrie definiert hat, legt er zunächst weitere grundsätzliche Voraussetzungen seines geometrischen Systems in einer kleinen Zahl von Axiomen (als richtig erkannte Grundsätze) und Postulaten (Festlegung weiterer Grundsätze) fest. Ausgehend von diesen Grundlagen folgen dann im weiteren Verlauf dieses Buches Theoreme und Konstruktionsaufgaben, in denen jeweils nur benutzt wird, was zuvor (in den Grundlagen beziehungsweise in vorausgehenden Theoremen und Konstruktionsaufgaben) bereits als richtig beziehungsweise möglich bewiesen wurde. Die danach folgenden Bücher bauen hierauf auf und behandeln jeweils bestimmte thematische Bereiche der Geometrie, wie zum Beispiel Eigenschaften von Kreisen (Buch III), Proportionen (Buch V) oder geometrische Folgen (Buch IX).

Das von Euklid formulierte mathematische System wurde offenbar bereits zu seiner Ent­stehungszeit als eine so deutliche Verbesserung gegenüber anderen derartigen Sammlungen wahrgenommen, dass es alle früheren Werke, von deren Existenz wir nur noch durch Kommentatoren wie den neuplatonischen Philosophen Proklus wissen, verdrängte. Diese Begeisterung hielt über Jahrhunderte an, sodass der Mathematikhistoriker Carl B. Boyer in seinem Überblickswerk A History of Mathematics (John Wiley & Sons, 1991) die Zahl der seit 1482 gedruckten Editionen (die Elemente waren ein Werk, das bereits früh gedruckt wurde!) mit mindestens 1000 angab und schätze, dass vermutlich außer der Bibel kein anderes Buch einen vergleichbaren Einfluss gehabt hat.

Vielleicht war es dieser Erfolg von Euklids Elementen, der der Mathematik auch prominenten Eingang in die Naturwissenschaften verschaffte – in den Worten von Galileo Galilei: »Das Buch der Natur ist in der Sprache der Mathematik geschrieben.« Diejenigen Naturwissenschaften, deren Gesetze sich quantitativ genau, also mathematisch ausdrücken lassen (wie zum Beispiel die Physik), bekamen das Prädikat der »exakten Wissenschaften«. Die Ordnung von Beobachtungen durch die mathematische Erfassung und Auswertung von Daten ist seither ein selbstverständlicher Begleiter nicht nur in den Wissenschaften, sondern auch in unserem Alltag geworden, wie unter anderem das Buch des Mathematikers aus Cambridge, Thomas W. Körner, The Pleasures of Counting (Cambridge University Press, 1996) auf mehr als 500 Seiten illustriert. So halfen die mathematischen Techniken der Statistik und Kartierung Dr. John Snow im 19. Jahrhundert, die Ausbreitung der Cholera in London zu erforschen und zu bekämpfen. Für den Cholera-Ausbruch 1848 /49 erstellte er eine Tabelle der Todes­zahlen in den verschiedenen Distrikten, versah sie mit der Information zum jeweiligen Wasserversorger und überprüfte so seine Theorie vom Zusammenhang zwischen der Verbreitung der Cholera und der Aufnahme von kontaminiertem Wasser. In der darauffolgenden Epidemie in den Jahren 1853 /54 kartierte er die Cholerafälle und konnte sie so einer bestimmten öffent­lichen Wasserpumpe auf der Broad Street zuordnen. Auf Snows Empfehlung hin wurde der Griff ­dieser Pumpe entfernt – und die Cholera­fälle gingen zurück.

Grenzen der Mathematik in einer komplexen Welt

Auch in der Coronapandemie der vergangenen drei Jahre war die Mathematik allgegenwärtig. Viele von uns erinnern sich noch daran, wie Bundeskanzlerin Angela Merkel das exponentielle Wachstum erklärt hat, oder daran, wie der damalige Leiter des Robert Koch-Instituts Lothar Wieler die täglichen Inzidenzen und damit variierenden Gebote und Verbote erläuterte. Hier zeigten sich aber auch die Grenzen des Werkzeugs Mathematik bei der Schaffung von Ordnungen: Während die Mathematik mit der Zeit immer differenziertere Techniken zur Erfassung, Ordnung und damit auch der Interpretation von Daten unserer Umwelt geliefert hat, gibt sie weder eine Garantie noch eine Anleitung für deren – im Sinne des pharaonischen Ägypten – »maatgerechte«, also bestmögliche Nutzung, denn diese wäre auf anderer Ebene auszuhandeln. Dass diese Aushandlungsprozesse hochgradig komplex sind und nicht allein von Prinzipien abhängen, die aus naturwissenschaftlichen Erkenntnissen und grundlegenden ethischen Überlegungen abzuleiten wären, sondern zum Beispiel oft auch eine (über)mächtige ökono­mische Komponente beinhalten, ist nicht nur in der Coronapandemie spürbar geworden, sondern es zeigt sich auch aktuell im Umgang mit der Klimakrise.